Lossless compression is a family of techniques to compress or encode a given random data or source. It is sometimes called as source coding or entropy coding in literature. The term "entropy coding" stems from Shannon's source coding theorem, informally stated as follows.

In other words, if $x$ is losslessly compressed to $m$, then entropy is preserved. i.e. $\mathbb{H}[x] = \mathbb{H}[m]$. The source coding theorem imposes a fundamental limit on a given data or message up to which it can be compressed without any loss in information. In literature the compressed mapping $m_k$ of each possible outcome $a_k$ is called as the codeword. The above limit specifies the smallest theoretical length of the codeword in bits. An example of a common entropy coding method is the Huffman coding.

A Huffman coding is a simple method where the given outcomes are mapped directly to codewords uniquely. However, the crux of the method that makes it close in on the information limit is that it employs variable lengths for each codeword depending on its probability $p(x = a_k)$. More probable an outcome, smaller is its code length and vice versa. For a good explanation of the Huffman coding, refer to Chris Olah's article.

In the recent years, there has been much development in newer entropy coding techniques that perform better than Huffman coding ^[1]. In this post, we shall take a practical approach to study one recent entropy coding method - the Asymmetric Numeral Coding.

Problem Setup

Problem : Let us say you are keeping track of an incoming stream of bits on a small piece of paper. Obviously there is no room on the piece of paper to write down all the bits. How do you then keep track of it? By keeping track we mean that at any given moment, your log must reflect all of the past information.

Assume that we start tracking the bit at time step $i$ (represented as $b_i$) with an initial symbol $x_i$. When the next bit $b_{i+1}$ comes in, we must update our symbol to $x_{i+1}$. One simple way to update this is start with $x_0 = 2^0 = 1$ and at each time step, update $x_i$ as $$ x_{i+1} = C_1(x_i, b_{i+1}) = x_i + b_{i+1} \times 2^{i+1} $$

This essentially results in the decimal representation of $b_{i+1}b_{i}...b_2b_1$. This method, apart from being lossless and fast (powers of 2 can be computed using bit-shifts), has an interesting property - the range of values is being altered at every time step. Note that in the above equation, the incoming bit $b_{i+1}$ is being added to the most significant-bit (MSB) of $x_{i}$. Therefore, each such update increases the range.

Alternatively, the incoming bit can be added to the least significant-bit (LSB) such that the range is kept the same but the number alternates between odd and even (even number if $b_{i+1}$ is 0 and odd if 1). This can be written as

$$ x_{i+1} = C_2(x_i, b_{i+1}) = 2x_i + b_{i+1} $$

In other words, $b_{i+1}$ determines whether $x_{i+1}$ will be even or odd. In entropy coding, equation (2) is used in the well-known Arithmetic Coding (AC) technique while equation (3) is used in Asymmetric Numeral Systems(ANS). AC requires that the bits come in from LSB to MSB, while ANS requires from MSB to LSB. This fundamental difference lies in they way they are implemented. By default, all streaming data comes from MSB to LSB - AC implements like a queue (first-in-first-out) while ANS implements like a stack (last-in-first-out). Note that both methods are equally fast - both $2^{i+1}$ and $2x_{i}$ can be computed through bit-shift operations.

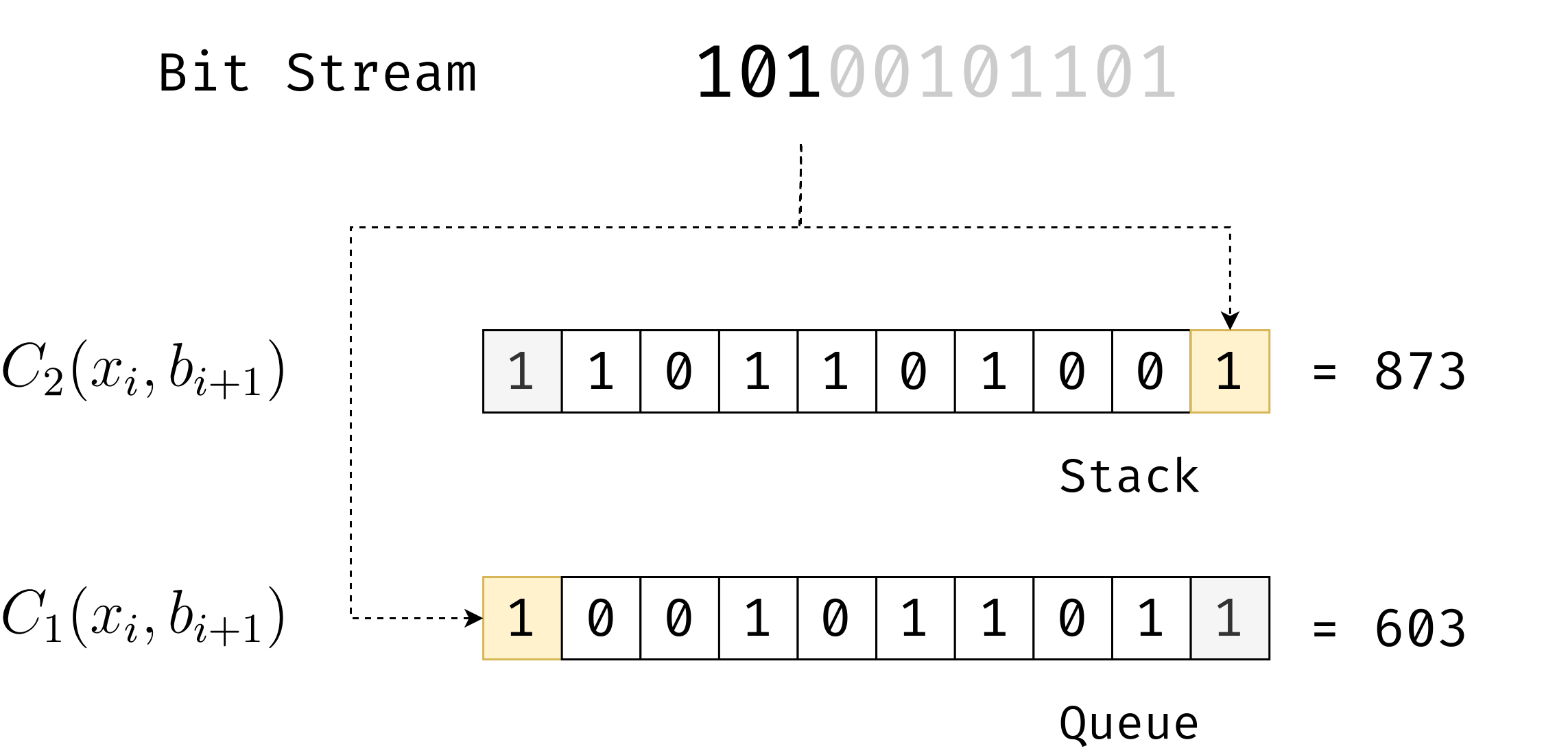
The fundamental idea behind both is that, given a symbol $x_i$, if one needs to add an incoming bit $b_{i+1}$ without any loss in information, any coding method should increase the information content should increase no more than the information content in the incoming bit.

$$ \begin{aligned} \log_2(x_{i+1}) &= \log_2(x_i) - \log_2(p(b)) \\ &= \log_2 \bigg ( \frac{x_i}{p(b)} \bigg ) \end{aligned} $$

Where $p(b)$ is the probability distribution of the bits. This means that any encoding function $C$ must be of the form $$C \approx x_i/p(b) $$ If the bits are equally probable, i.e. $p(b = 1) = p(b=0) = 1/2$, then the equation (3) is optimal in the sense that it satisfies the encoding condition $\big (C_1(x_i, b_{i+1}) \approx 2x_i \big )$.

The decoding function $D_2(x_{i+1})$ for $C_2$ can be constructed as

$$ D_2(x_{i+1}) = (x_i, b_{i+1}) = \bigg ( \bigg \lfloor \frac{x_{i+1}}{2} \bigg \rfloor, \bmod( x_{i+1}, 2) \bigg ) $$

A point to note here is that neither of the above two encodings are optimal as they are at least 1 bit larger than the shannon entropy. This is because we start with $x_0=1$. This is to differentiate '0' from '00' etc.

An easily overlooked aspect about the above encodings is that they amortize the coded result over the bits. That is, each bit is not mapped to one number, rather a bunch of bits are mapped into a single number. There is no one-to-one mapping, rather the information is distributed over the entire codeword. Therefore it has potential to be better than bit $\leftrightarrow$ number mapping. This amortization is the basis for all entropy coding methods as it indicates a potential technique get close to the Shannon entropy of the input ^[2].

# Code for binary -> natural number coding
# Bit Tricks: 
#   (a << b) <=> a * (2 ** b)
#   (a >> b) <=> a / (2 ** b)
#   (a % (2 ** b)) <=> (a & ((1 << b) - 1))

def C2(bitstream):  # Encode 
    """
    Encodes a list of bits (given in reverse order) to a Natural number.
    Ex: bitstream = [1, 0, 0, 1, 0, 1, 1, 0, 1].reverse() -> 873

    """
    x = 1
    for b in bitstream:
        x = (x << 1) + b 
    return x

def D2(x):  # Decode
    """
    Decodes the given coding into a list of bits.
    Ex: x = 873 -> [1, 0, 0, 1, 0, 1, 1, 0, 1]
    """

    bits= []
    while x > 1:
        bits.append(x % 2)
        x = x >> 1    
    return bits

# We convert binary to decimal here. Is it possible change the base? 
# Can you encode using different bases at each time step?

Asymmetric Numeral Coding

Asymmetric Numeral System (ANS) builds upon the $C_2 - D_2$ coding scheme and generalizes it. The above two coding schemes are sometimes referred as Positional Numeral Systems (PNS) and ANS can be viewed as the generalization of positional numeral systems. One concern in the PNS scheme is that $x$ must have a finite range. As the bits keep coming in, $x_i$ cannot be arbitrarily large in practice. Thus we need to address two issues -

1. Enforcing $x$ to be within some finite interval of natural numbers.
2. Within that finite interval, the distribution of even and odd codings must reflect the corresponding probabilities of the bits. Let's address the latter issue first.

Consider equation (3) again. As discussed earlier, it is optimal only when $p(b = 0) = p(b=1) = 1/2$. We can say that the bit probability splits and uniformly covers the range of $x$, which is the set of all natural numbers $\mathbb{N}$. In the case $p(b=1) = 1/2$, the range is split into two parts - even and odd numbers depending on the value of $b$. As such $x_{i+1}$ is the $x_i^{th}$ number in the even/odd set.

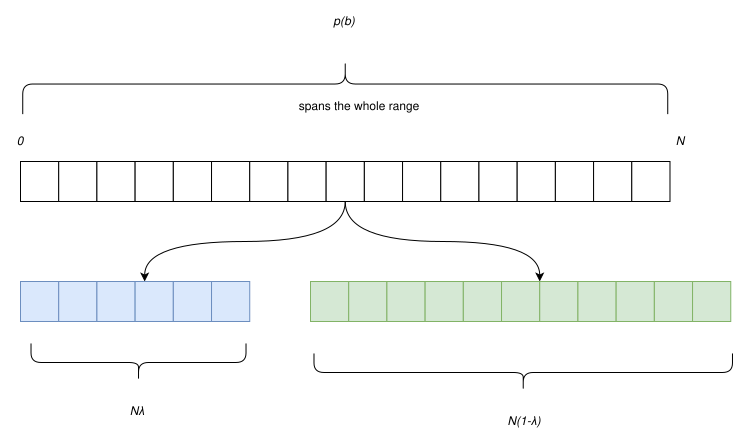
Extending this intuition to unequal probabilities, $x_{i+1}$ is the $x_{i}^{th}$ number in the subset defined by $b_{i+1}$. For this, the range of $x$ must be split into two subsets whose size reflects the probability of thier respective state. If the probability of 1 is $p(b = 1) = \lambda < p(b= 0) = (1 - \lambda)$ and let the range of $x$ be the set $\fF = [0, N]$, then we want $ \lceil N\lambda \rceil$ odd numbers in $\fF$. The $\lceil \cdot \rceil$ operator accounts for the fractional components as we shall stick to natural numbers. We want a generalized coding method such that the following equality is satisfied.

$$ \lceil (x_{i+1} + 1) \lambda \rceil - \lceil x_{i+1} \lambda \rceil = b_{i+1} $$

Say we updated $x_i \to x_{i+1}$ using some encoding. Now, the proportion of odds is $\lceil x_{i+1} \lambda \rceil$. However, the coding must be robust to the ceil operation. For example, for $b_{i+1} = 0, \lambda = 0.3$ say we compute $x_{i+1} = 6$, then we have $\lceil 6 * 0.3 \rceil = 2$ odd values in the range (0,6]. Now $\lceil (6 + 1) * 0.3 \rceil = 3 $ which means $\lceil (6 + 1) * 0.3 \rceil - \lceil 6 * 0.3 \rceil = 1 \neq 0$. Therefore, $x_{i+1} = 6$ cannot be a correct code for $b_{i+1} = 0, \lambda = 0.3$. On the other hand, $x_{i+1} = 9$ is a valid code and can be verified similarly. The idea behind equation (7) is that by doing ceil operation (we will use more of those below), we are essentially rounding the computation results; and when done sequentially, the error may blow up resulting in incorrect code that may not be uniquely reversible i.e. loss of information.

We can now come up with a coding scheme that accounts for any arbitrary binary distribution $p$, satisfying equation (7). If the probability of 1 is $p(b = 1) = \lambda < p(b = 0) = (1 - \lambda)$, then

$$ x_{i+1} = C_2(x_i, b_{i+1}) = \begin{cases} \big \lceil \frac{x_i + 1}{1 - \lambda} \big \rceil -1 &; b_{i+1} = 0 \\ \big \lfloor \frac{x_i}{\lambda} \big \rfloor &; b_{i+1} = 1 \\ \end{cases} $$

It is easy to verify the above equation with equation (3) for $\lambda=1/2$. The decoding function $D_2$ can be derived as

$$ \begin{aligned} D_2(x_{i+1}) &= (x_i, b_{i+1}) \\ x_i &= \begin{cases} \lceil x_{i+1} \lambda \rceil &; b_{i+1} = 1 \\ x_{i+1} - \lceil x_{i+1} \lambda \rceil &; b_{i+1} = 0 \end{cases} \\ b_{i+1} &= \lceil (x_{i+1} + 1) \lambda \rceil - \lceil x_{i+1} \lambda \rceil \end{aligned} $$

Observe that decoding $b_{i+1}$ is essentially through equation (7). The above encoding scheme is called as uniform Asymmetric Binary Systems (uABS) as we exploit the asymmetry in the probabilities of the bits to get compression, while the subsets segmented by those probabilities are themselves uniformly distributed.

Let us take an illustrative example - Consider the bitstream 1, 0, 0, 1, 0 with $p(b =1) = \lambda = 0.3$. This can be encoded using equation (8) as follows (note that we encode in the reverse order)

$$ \begin{aligned} x_0 & &&= 1 \\ x_1 &= \bigg \lceil \frac{x_0 + 1}{0.7} \bigg \rceil -1 &&= 2 &&& (b_1 = 0) \\ x_2 &= \bigg\lceil \frac{x_{1}}{0.3} \bigg \rceil &&= 6 &&& (b_2 = 1) \\ x_3 &= \bigg \lceil \frac{x_2 + 1}{0.7} \bigg \rceil -1 &&= 9 &&& (b_3 = 0) \\ x_4 &= \bigg \lceil \frac{x_3 + 1}{0.7} \bigg \rceil -1 &&= 14 &&& (b_4 = 0) \\ x_5 &= \bigg\lceil \frac{x_{4}}{0.3} \bigg \rceil &&= 46 &&& (b_5 = 1) \\ \end{aligned} $$

Similarly decoding can be done as

$$ \begin{aligned} & &&x_5 &&&= 46 \\ b_5 &= \lceil (x_5 + 1) \x 0.3 \rceil - \lceil x_5 \x 0.3 \rceil = 1; &&x_4 = x_5 - \lceil x_5 \x 0.3 \rceil &&&=14 \\ b_4 &= \lceil (x_4 + 1) \x 0.3 \rceil - \lceil x_4 \x 0.3 \rceil = 0; &&x_3 = \lceil x_4 \x 0.3 \rceil &&&=9 \\ b_3 &= \lceil (x_2 + 1) \x 0.3 \rceil - \lceil x_2 \x 0.3 \rceil = 0; &&x_2= \lceil x_3 \x 0.3 \rceil &&&=6 \\ b_2 &= \lceil (x_2 + 1) \x 0.3 \rceil - \lceil x_2 \x 0.3 \rceil = 1; &&x_1 = x_2 - \lceil x_2 \x 0.3 \rceil &&&=2 \\ b_1 &= \lceil (x_1 + 1) \x 0.3 \rceil - \lceil x_1 \x 0.3 \rceil = 0; &&x_0= \lceil x_1 \x 0.3 \rceil &&&=1\\ \end{aligned} $$

And we get back our code in its original order.

# Code for generalized binary -> natural number coding
import math

def C2(bitstream, p: float = 0.5):  # Encode
    """
    Encodes a list of bits (given in reverse order) to a
    Natural number with probability p.
    """
    x = 1
    for b in bitstream:
        if b:
            x = math.floor(x / p)
        else:
            x = math.ceil((x + 1) / (1 - p)) - 1
    return x

def D2(x, p:float = 0.5):  # Decode
    """
    Decodes the given coding into a list of bits with probability p.
    """

    bits= []
    while x > 1:
        b = math.ceil((x + 1) * p) - math.ceil(x * p)
        bits.append(b)
        if b:
            x = math.ceil(x * p)
        else:
            x = x - math.ceil(x * p)
    return bits

# What happens if you give a bitstream of length 60 or more? 
# Does it decode correctly? Why? 

Extending to Arbitrary Alphabets

Now it is important to see the bits in the above discussion as a set containing just two symbols $\fB = \{0, 1\}$. This set is called as the alphabet set. The above discussion pertaining to binary alphabets can be extended to any alphabet set $\fA = \{a_1, ...,a_K \}$ of $K$ elements with an associated probability distribution $p$ over all its symbols. Based on the previous discussion, given the range for the encoding as $(0, M]$ (where $M = 2^r$), which is a part of the natural number range $\mathbb{N}$, we ideally have to split the range into $K$ disjoint regions each with size proportional to the respective symbol probabilities. In other words, we want to split the range into $f_1,f_2, ..., f_K$ where

$$ \begin{aligned} f_k &= p(s = a_k) M \quad k = 1, ...,K \

\sum_{k=1}^K f_k &= M \end{aligned} $$ These range sizes $f_k$ are called as _scaled probabilities_. To construct a coding scheme, we must ensure that $x_{i+1}$ is the $x_i^{th}$ value in the $k^{th}$ subset, given the symbol $a_k$. This is a direct extension of the idea discussed earlier for even - odd subsets.

Recall equation (3). It can be interpreted as follows $-$ $b_{i+1}$ essentially chooses the odd or even subsets and $2x_i$ adds the necessary offset within that subset. Therefore, our required generalized mechanism can be written in the form $$ x_{i+1} = C_{ANS}(x_i, s_{i+1}) = \text{Offset } + \text{ Subset selection}

$$ Where $s_{i+1}$ is the input symbol that can take values in ${a_1, ..., a_K}$. One core insight here is that the values in the subsets of size $f_k$ are uniformly distributed. Each value within those subsets are equally likely. This makes our offset computation much simpler.

Let $x_i$ be the current state and the incoming symbol be $s_{i+1} = a_k$. The offset can be calculated as $$ M\bigg \lfloor \frac{x_i}{f_k} \bigg \rfloor + \bmod(x_i, f_k) $$ The precise location within the $k^{th}$ subset is calculated by $\bmod(x_i, f_k)$. This is because $k^{th}$ subset has a fixed size and using modulus helps us recycle the values within the subset. This step is essential to avoid a massive value for $M$. However, this recycling destroys the uniqueness of the encoding. We must therefore, repeat the range of size $M$ over the natural number range $\mathbb{N}$ (Refer the above figure). We can then uniquely identify the range of size $M$ within the natural number range by $ M\bigg \lfloor \frac{x_i}{f_k} \bigg \rfloor $.

The subset selection part is pretty straightforward. Each symbol in the alphabet $\fA$ that occurs before $a_k$ occupies $f_1, f_2, .. f_{k-1}$ points on $(0,M]$ respectively. If we wish to select the $k^{th}$ subset, then its starting point is simply

$$ \sum_{j=1}^{k-1} f_j = CDF(a_k) $$

This is essentially the CDF of the symbol $a_k$ as $f_1, ... f_K$ are now viewed as scaled probabilities. Putting everything together, we get the final ANS coding scheme. $$ x_{i+1} = C_{ANS}(x_i, s_{i+1})= M\bigg \lfloor \frac{x_i}{f_k} \bigg \rfloor +\bmod (x_i, f_k) +\sum_{j=1}^{k-1} f_j $$

Decoding can be done simply by inverting each of the encoding components. $$ \begin{aligned} D_{ANS}(x_{i+1}) & = (x_i, s_{i+1}) \\ x_i &= f_k \bigg \lfloor \frac{x_{i+1}}{M} \bigg \rfloor - \sum_{j=1}^{k-1} f_j + \bmod(x_{i+1}, M) \\ s_{i+1} &= \bmod(x_{i+1}, M) \quad s.t \quad CDF(a_k) \leq \bmod(x_{i+1}, M) < CDF(a_{k+1}) \end{aligned} $$ The latter part of the above equation can be computed easily through pre-computing the inverse cumulative distribution function. This can understandably be non-trivial to compute in some cases. In such cases there are more sophisticated techniques available. In this discussion, we shall stick to a simple iterative method to find the symbol $s_{i+1}$ that satisfies the above constraint.

Implementation

class rANS:
    """
    Bit Tricks:
      (a << b) <=> a * (2 ** b)
      (a >> b) <=> a / (2 ** b)
      (a % (2 ** b)) <=> (a & ((1 << b) - 1))
    """
    def __init__(self,
                 precision: int,
                 alphabet: List[str],
                 probs: List[int],
                 verbose: bool = False) -> None:
        """
        Implements the rANS as a stack.
        Encoding and Decoding are named as 'push'
        and 'pop' operations to be consistent with
        stack terms.

        Usage:
            rans = rANS(precision, Alphabet, probs)
            rans.push(symbol)
            decoded_symbol = rand.pop()
        """
        assert precision > 0
        self.precision = precision
        self.verbose = verbose

        self.Alphabet = alphabet
        scaled_probs = probs * (1 << precision)
        cum_probs = np.insert(np.cumsum(scaled_probs), 0, 0)

        # Make sure everything is an int
        scaled_probs = scaled_probs.astype(np.int64)
        cum_probs = cum_probs.astype(np.int64)

        self.probs = dict(zip(A, probs)) # Python 3.7 Dicts are ordered
        self.fk = dict(zip(A, scaled_probs))
        self.cdf = dict(zip(A, cum_probs))

        self.x = 1      # State

    def push(self, symbol: str):    # Encode
        """
        Coding formula:
            M floor(x / Fk) + CDF(symbol) + (x mod Fk)
        :param s: Symbol
        """
        if (self.x // self.fk[symbol] << self.precision):

        self.x = ((self.x // self.fk[symbol] << self.precision)
                  + self.x % self.fk[symbol]
                  + self.cdf[symbol])

    def pop(self) -> str:   # Decode
        """
        Decoding formula:
            symbol = (x mod M) such that CDF(symbol) <= (x mod M) < CDF(symbol + 1)
            x = floor(x / M) fk - CDF(symbol) (x mod M)
        :return: Decoded symbol
        """
        cdf = self.x & ((1 << self.precision) - 1)
        symbol = self._icdf(cdf)
        self.x = ((self.x >> self.precision) * self.fk[symbol]
                  - self.cdf[symbol]
                  + cdf)
        return symbol

    def _icdf(self, value: int) -> str :
        result = None
        prev_symbol,prev_cdf = list(self.cdf.items())[0]
        for symbol, cdf in list(self.cdf.items())[1:]:
            if prev_cdf <= value < cdf:
                result= prev_symbol
            prev_symbol,prev_cdf = symbol, cdf

        return result if result else self.Alphabet[-1]  # Account for the last subset

Conclusion

We have discussed ANS from the fundamentals of information theory and hopefully with some good intuition. We have however, ignored one crucial part which makes ANS practical. It is easy to observe that as the stream of symbols becomes longer, the range required to encode them also increases exponentially (in the order of $2^N$ where $N$ is the number of symbols in the stream). This can quickly become infeasible. This can be resolved through a process called renormalization where $x_i$ is normalized to be within some fixed range in some appropriate precision^[3]. In a future post, we shall revisit ANS from a practical perspective.

References & Further Reading

For a detailed discussion of all the above described methods, refer James Townsend's PhD thesis. Additionally, his tutorial provides some implementation details of ANS along with a Python code.

Another accessible article on ANS was written by Brian Keng.

For an authentic source Jarek Duda, the inventor of ANS, has published a very nice overview on ANS.

A detailed tutorial on ANS is available on YouTube by Robert Bamler of the University of Tübingen as a part of his course on "Data compression with deep probabilistic models".