With the success of text-to-image models, the natural next step has been to generate videos - visually pleasing, temporally coherent, and geometrically consistent. As such, the past year or so has been abound with such video generation models with carefully crafted techniques and interestingly, a nice way of parameterizing the camera viewpoints. This parameterization^[1], using Plücker coordinates has become quite popular among the recent learning-based methods for view and novel view synthesis tasks.

Plücker coordinates are essentially a way of parameterizing lines^[2]. The Plücker coordinates of a given ray $l$ with unit direction $\vd \in \S^3$ through a point $\vp \in \R^3$ is given by

$$l:= (\vp, \vn) \in \R^6; \qquad \vn = \vp \times \vd$$

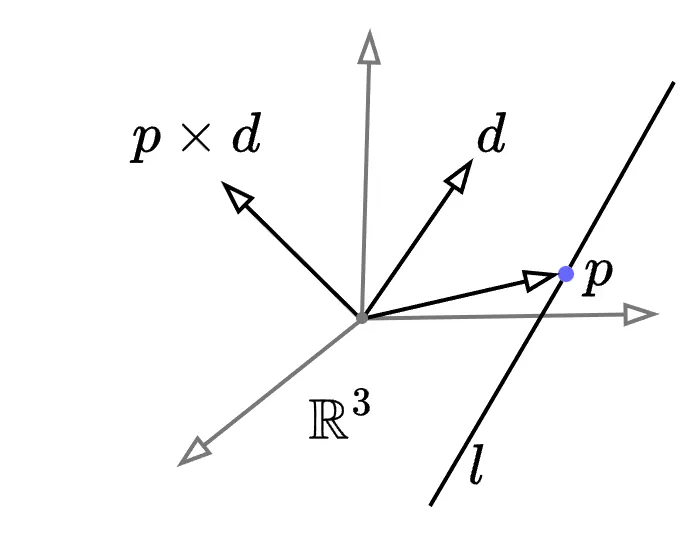
Plücker coordinates parameterizing the ray $l$.

The vector $\vn$, called the $moment$, is orthogonal to the plane containing the ray $l$ and the origin. If $\vn=0$, then the ray passes through the origin and is defined only its direction $\vd$. A quick note: observe that the above Plücker coordinates are 6 dimensional, while a line in 3D only requires 4 dimensions to completely represent it. But, we also have the constraint $\vn^T\vp = 0$. Reconciling these two, we note that the Plücker coordinates lie on a curved 4-dimensional manifold in $\R^6$.

Plücker coordinates are invariant to scaling i.e. $(\vp , \vn) = \lambda (\vp , \vn); \lambda > 0$ as the line itself does not change. Furthermore, the Plücker coordinate is independent of the choice of point $\vp$. Plücker coordinates also provide elegant ways of computing angles, signed distances between rays and more. With such convenient geometric calculations, Plücker coordinates were so far quite popular in robotics.

  The use of Plücker coordinates in camera projection and multi-view geometry is actually well-studied, described in Hartley and Zisserman's book Multiple View Geometry in Computer Vision. The idea there is to parameterize 3D lines in the world onto the image plane using Plücker coordinates. Such lines can then be used for camera calibration, and this technique has been used for in-the-wild camera calibration without the need for pre-calibrated markers. On the other hand, camera parameterization using Plücker coordinates is relatively a recent development, where the light rays incident on the image plane are parameterized. In other words, the camera is parameterized by all the incident rays, and can be thought as a representation of the real 3D scene.

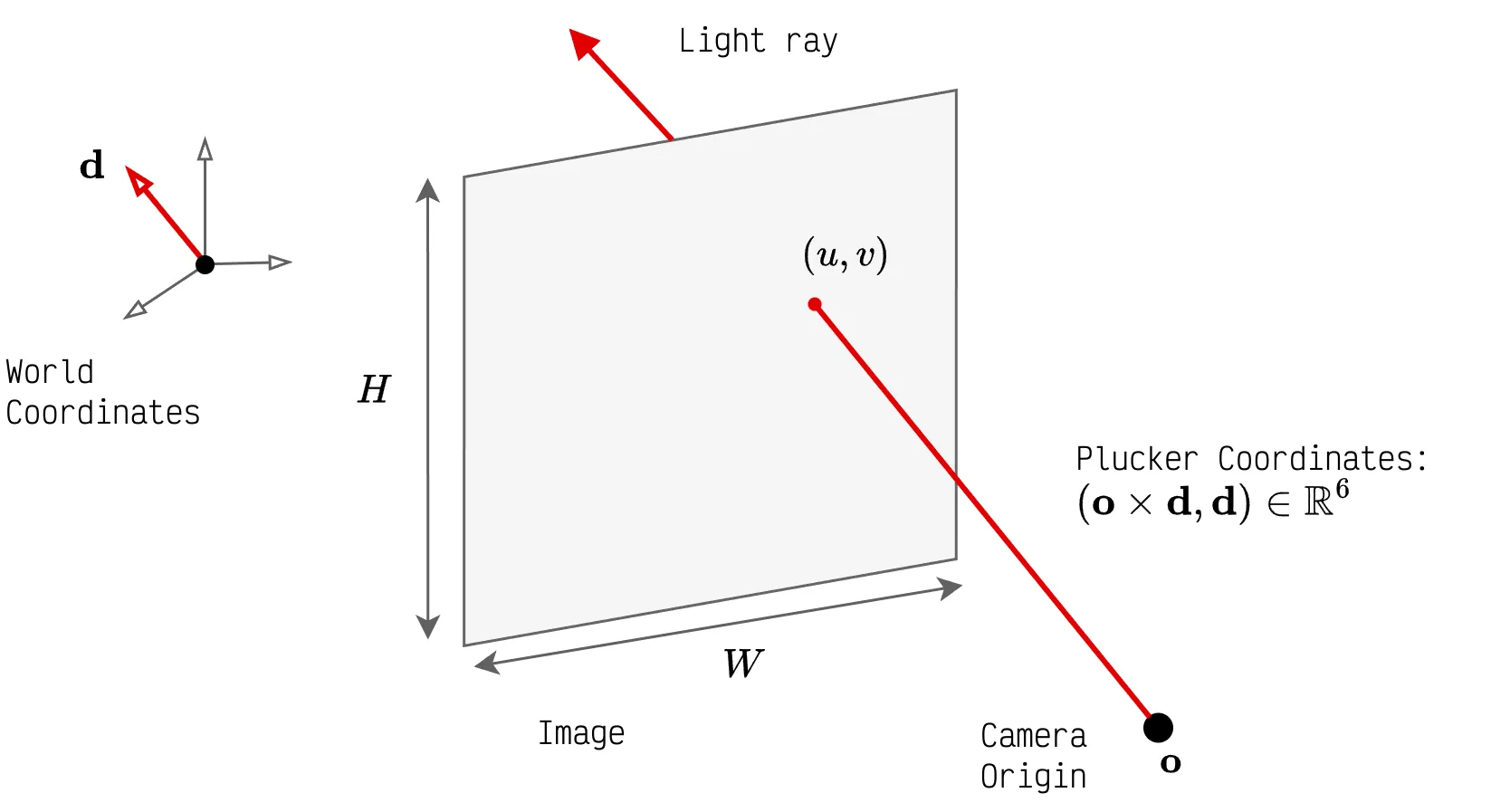
Consider the scenario where the image $\fI$ of size $H \times W$ and the camera parameters are known, including intrinsics $\vK \in \R^{3 \times 3}$ (mapping from camera coordinates to the pixel coordinates) and extrinsic pose $\vE=[\vR; \vt] \in \R^{3 \times 4}$ (mapping from the world coordinates to camera coordinates) where $\vR \in \R^{3 \times 3}$ is the rotation matrix and $\vt \in \R^{3 \times 1}$ is the translation vector. Then, the pixel value at $(u, v)$ on the image represents the intensity of the light ray incident at that position on the film as captured by the camera. The unit direction vector $\vd$ of that light ray can be reconstructed in the world coordinates as

$$\begin{aligned} \vd'&=\vR\vK^{-1} \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} + \vt ; \qquad \; (\vR^{-1} = \vR^T) \\ \vd &= \frac{\vd'}{\|\vd'\|} \end{aligned}$$

The above ray passes through the camera focal point (origin) as well the pixel coordinates $(u, v)$ in the world coordinate frame as shown by the figure above. Given this direction vector, the moment vector $\vn$ can can be computed as the cross product between the camera origin and the direction vector.

$$\vn = \vo \x \vd$$

The Plücker coordinates for the incident ray is a 6-tuple $(\vn, \vd)$. Based on this, the Plücker camera parameterization can be constructed as the set of Plücker coordinates of all the rays, i.e. $\R^{HW \x 6}$.

Although the Plücker camera parameterization has too many parameters compared to the usual intrinsic-extrinsic matrices, there are quite a few advantages — 1) it is complete i.e can uniformly represent all incident light rays in the scene uniformly; 2) The invariance to scaling, and the invariance to the selection of point on the ray, means that these coordinates are indeed homogeneous; 3) It is smooth and differentiable.

The above characteristics make Plücker camera parameterization quite suitable for learning-based methods.

Code

import torch

def convert_to_plucker(K_inv: torch.Tensor,
                       M_inv: torch.Tensor,
                       H: int,
                       W: int) -> torch.Tensor:
    """
    Function to compute the  Plucker coordinates for the camera based on the
    rays incident on the image plane, using the camera's
    intrinsic and extrinsic parameters.

    Args:
        K_inv: (torch.Tensor) Inverse of the c3x3 amera intrinsic matrix.
        M_inv: (torch.Tensor) Inverse of the 4x4 camera extrinsic matrix
               (camera-to-world transform).
        H: (int) Height of the image in pixels.
        W: (int) Width of the image in pixels.

    Returns:
        Tuple containing:
            plucker_coords: torch.Tensor
                Plucker coordinates for each ray. Shape (H, W, 6).
            uv_world: torch.Tensor
                Image grid points in world coordinates. Shape (H, W, 3).
            d: torch.Tensor
                Normalized ray directions in camera space. Shape (H, W, 3).
            o_world: torch.Tensor
                Camera origin in world coordinates. Shape (3,).
    """

    Rot, trans = M_inv[:3, :3], M_inv[:3, 3:]
    # create image grid
    u, v = torch.meshgrid(
        torch.arange(W, dtype=torch.float32),
        torch.arange(H, dtype=torch.float32),
        indexing='xy',
    )

    uv = torch.dstack([u, v, torch.ones_like(u)]) # (H, W, 2)

    d =  Rot[None, None,] @ (K_inv[None, None, ...] @ uv.unsqueeze(-1)) \
         + trans[None, None]

    # Normalize the ray direction to get a unit direction vector
    d = d / torch.linalg.norm(d, dim=-2, keepdim=True)

    # Camera origin in world coordinates
    o_world = M_inv[...,:3, 3]
    # uv in world coordinates
    uv_world = uv @ Rot + o_world

    # convert d to world coordinates
    d_world = (M_inv[:3, :3] @ d + trans).squeeze(-1)

    # compute the moment
    n = torch.cross(o_world.expand_as(d_world), d_world, dim=-1)

    plucker_coords = torch.cat([n, d_world], dim=-1)

    return plucker_coords
Copy