Novel-View Synthesis (NVS) is a tricky problem. Given a set of images of a scene, the aim is to synthesize new images of the same scene with new perspectives not present in the given set. A more extreme form of this problem is to generate new perspectives (camera viewpoints) from a single image.
If we have the camera parameters for the image, then a potential solution is to modify the camera parameters and reproject the scene to yield the corresponding image. However, we do not know the 3D scene beforehand and reconstructing it requires multi-view images, leading to a circular dependency.
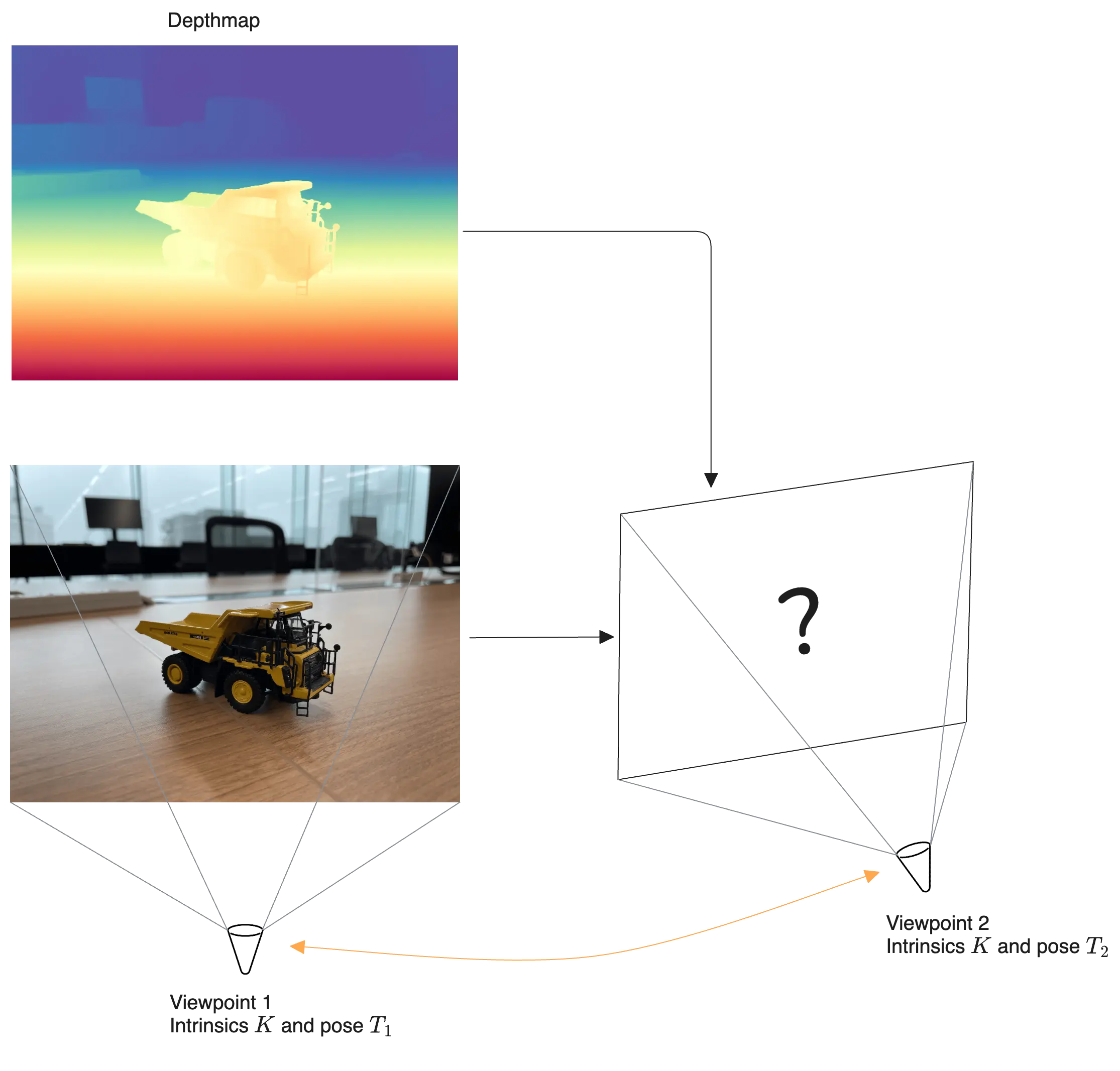
While estimating camera parameters can itself be challenging[1], we will assume that the camera intrinsics are provided but the camera pose itself can be arbitrary. Modern techniques like MoGe can also provide both the depth map and an estimate for the camera intrinsics for the given image.
Consider the following alternative idea given a perspective image of the scene, its camera parameters , and its corresponding depth-map , the goal is to generate different perspectives of the same scene with the depth information intact. This can be seen as the first step of a NVS pipeline[2] where the different perspectives of the scene (estimated based on the depth-map) are then inpainted, thanks to the amazing diffusion models, to get the final result.

Perspective transformation results in depth-based pixel translation. Source: matousekfoto - Freeman Alley Dataset.
But before we jump into solving the problem, let's quickly check if the new proposal is even reasonable to begin with? When a scene is captured from two different camera viewpoints (as shown in the figure above), various objects in the image are transformed based on their distance to the camera and movement of the camera from the first position to the next. Note that we already know the camera transformation from one position to the next based on their extrinsic matrices. Since the depth-map provides the necessary relative offsets between various objects in the scene, the problem can indeed be solved. In fact, this procedure can be thought as the inverse of the depth estimation from stereo images problem. In fact, this inverse problem is sometimes referred to as Depth-based Image Rendering or DBIR for short[3].
Depth-Based Image Rendering
Warping Images based on Depth
Say the given image has a depth map and camera parameters and . Given the new camera parameters and , we would like to reconstruct the warped image from the new view point. Practically, one may assume that two camera intrinsics are the same (), but we shall keep them distinct for generality.
The procedure broadly consists of two parts - 1) compute the optical flow (offset) describing how each pixel will move based on the new camera position and the depth information of each pixel; 2) Splat each pixel weighted by its offsets and the depth onto the resultant image.
Optical Flow based on Depth
Recall the camera projection equation, for a point in the (homogeneous) world coordinate, projected onto the camera coordinates as where is the camera intrinsic matrix and is the extrinsic matrix (in homogeneous coordinates) specifying the rotation and translation. To get the world coordinates from the camera coordinates, we can invert the above procedure by simply inverting the matrices. Note that the 3D camera camera coordinates of the first viewpoint can be obtained by scaling the pixels with the corresponding depth information .
This world coordinate can again be projected onto the second camera viewpoint as These camera coordinates can then be normalized by its coordinate (depth) to yield the pixel coordinates . Finally, the flow of pixels from the first viewpoint to the next is simply given by
import torch
def get_camera_transformation(depthmap:torch.Tensor,
K1:torch.Tensor,
K2:torch.Tensor,
M1:torch.Tensor,
M2:torch.Tensor,) -> torch.Tensor:
"""
This function returns the camera transformation matrix
between two given camera matrices and a depthmap. This is
done as follows -
Map the image coordinates from camera 1 (K1, M1) to the
world coordinates by inverse projection, and remap these
world coordinates onto the camera 1's (K2, M2) image
plane.
Args:
depthmap: Depth map tensor of shape (H, W)
K1: First Camera (3, 3) intrinsic matrix
K2: Second Camera (3, 3) intrinsic matrix
M1: First Camera (4, 4) extrinsic matrix
M2: Second Camera (4, 4) extrinsic matrix
Returns:
Transformation tensor that maps coordinates from the first
camera view to the second camera view
"""
height, width = depthmap.shape
# Get the transformation matrix from first viewpoint
# to the second view point.
T21 = M2 @ torch.linalg.inv(M1) # (4 x)
# Create homogeneous image coordinates for the
# camera viewpoint
uv_coords = get_uv_coords(height, width, is_homo=True) # (H, W, 1)
# Un-project the image coordinates to the world coordinates
K1_inv = torch.linalg.inv(K1)[None, None, ...] # (1, ,1, 3, 3)
world_coords = K1_inv @ uv_coords[..., None] # (H, W, 3, 1)
# scale the world coordinates by the depth
world_coords = depthmap[..., None, None] * world_coords # (H, W, 3, 1)
# Transform the world coordinates based on the transformation
# between the two cameras.
# but before that, make the world coords homogeneous
world_coords = torch.dstack([world_coords,
torch.ones(height, width)[..., None, None]]) # (H, W, 4, 1)
world_coords_trans = T21[None, None] @ world_coords
# (1, 1, 4, 4) @ (H, W, 4, 1) -> (H, W, 4, 1)
world_coords_trans = world_coords_trans[..., :3, :] # (H, W, 3, 1)
# Reproject the transformed world coordinates to the
# 2nd camera viewpoint
trans_coords = K2[None, None, ...] @ world_coords_trans
# (1, 1, 3, 3) @ (H, W, 3, 1) -> (H, W, 3, 1)
return trans_coords[..., 0] # ignore the last dim in the homogeneous form
def get_uv_coords(height:int,
width:int,
is_homo: bool = False) -> torch.Tensor:
"""
Helper function that returns the uv coordinates of the image.
Args:
height: Height of the image
width: Width of the image
is_homo: Whether to return the homogeneous coordinates
Returns:
uv_coords: UV coordinates of the image
"""
x_, y_= torch.meshgrid(torch.arange(width),
torch.arange(height),
indexing='xy')
# x_: (H, W)
# y_: (H, W)
uv_coords = torch.dstack([x_, y_]) # (H, W, 3)
if is_homo: # Add 1s to make homogeneous
ones = torch.ones_like(x_) # (H, w)
uv_coords = torch.dstack([uv_coords, ones]) # (H, W, 1)
return uv_coords.float()
Flowmap
Splatting
In its basic sense, the technique of splatting can be described as the weighted sum of the projected elements. These elements can be pixels, as in our case, or more sophisticated elements like 3D Gaussians, as in Gaussian splatting. In our case, the splatting function can be written as a function of the input image to be warped, the transformation of the pixels from the 1st camera viewpoint to the second (i.e the flowmap) and some weights .
Where operator represents the splatting/mapping of the weighted pixels into the transformed coordinates. Computing the pixel weights based on the depth is an interesting problem a simple inverse scaling such as weights all objects proportionally, resulting in farther objects being smeared and closer objects with good separation between them, even though the relative distances between them might be the same. A couple of common improvements to address this problem and reduce visual flickering are neighborhood scaling where the depth is the average of the neighbors from inverse bilinear interpolation[4] , and exponential scaling[5] .
def splat_points(image:torch.Tensor,
weights: torch.Tensor,
flowmap: torch.Tensor,
do_exp_weights: bool = False) -> Tuple[torch.Tensor, torch.Tensor]:
"""
Splat the image pixels onto the transformed positions as
dictated by the flowmap and the depth weights. This function uses
the inverse bilinear interpolation to construct the neighboring
pixels and then splats the image pixels onto the transformed positions.
Args:
image (torch.Tensor): Input image tensor of shape (H, W, C).
weights (torch.Tensor): Depth weights tensor of shape (H, W).
flowmap (torch.Tensor): Flow map tensor of shape (H, W, 2).
do_exp_weights (bool): Whether to use exponential weights.
Default is False.
Returns:
Tuple[torch.Tensor, torch.Tensor]: A tuple containing:
- splat_image (torch.Tensor): The splatted image tensor
of shape (H, W, C).
- mask (torch.Tensor): A mask tensor of shape (H, W)
indicating valid splatted pixels.
"""
if not torch.is_floating_point(image):
image = image.float()
height, width, channels = image.shape
# Step 1: Get the transformed positions
uv_coords = get_uv_coords(height, width) # (H, W, 2)
trans_coords = flowmap + uv_coords # (H, W, 2)
trans_coords = trans_coords + 1
trans_coords_low = torch.floor(trans_coords).long() # (H, W, 2)
trans_coords_high = torch.ceil(trans_coords).long() # (H, W, 2)
# Clamp the transformed coordinates to the image boundaries
trans_coords[..., 0].clamp_(min=0, max=width+1) # (H, W, 2)
trans_coords[..., 1].clamp_(min=0, max=height+1)
trans_coords_low[..., 0].clamp_(min=0, max=width+1)
trans_coords_low[..., 1].clamp_(min=0, max=height+1)
trans_coords_high[..., 0].clamp_(min=0, max=width+1)
trans_coords_high[..., 1].clamp_(min=0, max=height+1)
# Calculate the weights for the four neighboring pixels
# (Inverse bilinear interpolation)
# The neighboring pixels are defined as follows:
#
# (x_low, y_high) SW - - - - SE (x_high, y_high)
# | |
# | P |
# | (x, y) |
# | |
# (x_low, y_low) NW - - - - NE (x_high, y_low)
#
# P is the pixel we are interpolating
# NW, NE, SW, SE are the four neighboring pixels
x_offset_low = trans_coords[..., 0:1] - trans_coords_low[..., 0:1]
x_offset_high = trans_coords_high[..., 0:1] - trans_coords[..., 0:1]
y_offset_low = trans_coords[..., 1:2] - trans_coords_low[..., 1:2]
y_offset_high = trans_coords_high[..., 1:2] - trans_coords[..., 1:2]
flow_sw = (1 - x_offset_low) * (1 - y_offset_high) # (H, W, 1)
flow_se = (1 - x_offset_high) * (1 - y_offset_high) # (H, W, 1)
flow_nw = (1 - x_offset_low) * (1 - y_offset_low) # (H, W, 1)
flow_ne = (1 - x_offset_high) * (1 - y_offset_low) # (H, W, 1)
# Augment the flow offsets based on the depth weights
if do_exp_weights:
flow_sw = flow_sw * torch.exp(1.0 / weights)
flow_se = flow_se * torch.exp(1.0 / weights)
flow_nw = flow_nw * torch.exp(1.0 / weights)
flow_ne = flow_ne * torch.exp(1.0 / weights)
else:
flow_sw = flow_sw / weights
flow_se = flow_se / weights
flow_nw = flow_nw / weights
flow_ne = flow_ne / weights
# Splat the weighted pixel values into the transformed coordinates
# Note: We account for the overflow of the pixels beyond the image boundaries
# but we shall center crop it later.
splat_image = torch.zeros(size=(height + 2, width+2, channels)).to(image)
# Recall the splatting process is essentially a weighted sum of the image pixels
# based on the depth, mapped onto the transformed positions and then normalized.
# Numerator:
splat_image[trans_coords_high[..., 1], trans_coords_low[..., 0], :] += image * flow_sw
splat_image[trans_coords_high[...,1], trans_coords_high[..., 0], :] += image * flow_se
splat_image[trans_coords_low[...,1], trans_coords_low[..., 0], :] += image * flow_nw
splat_image[trans_coords_low[..., 1], trans_coords_high[..., 0], :] += image * flow_ne
# Denominator: accumulate the weights for normalization
weights_acc = torch.zeros(size=(height + 2, width +2, 1)).to(image)
weights_acc[trans_coords_high[..., 1], trans_coords_low[..., 0], :] += flow_sw
weights_acc[trans_coords_high[...,1], trans_coords_high[..., 0], :] += flow_se
weights_acc[trans_coords_low[...,1], trans_coords_low[..., 0], :] += flow_nw
weights_acc[trans_coords_low[..., 1], trans_coords_high[..., 0], :] += flow_ne
# Center crop the resultant splatted image and weights
cropped_splat_image = splat_image[1:-1, 1:-1, :]
cropped_weights = weights_acc[1:-1, 1:-1, :]
assert cropped_weights.max() > 0, f"{cropped_weights.min()}"
mask = cropped_weights > 0
# Normalize the splatted image
splat_image = torch.where(mask, cropped_splat_image / cropped_weights, 0.0)
return (splat_image, mask)
def forward_warping(image: torch.Tensor,
depthmap: torch.Tensor,
K1: torch.Tensor,
M1: torch.Tensor,
M2: torch.Tensor,
K2: Optional[torch.Tensor] = None,
gamma:float = 5.0) -> Tuple[torch.Tensor, torch.Tensor]:
""""
Warp the given image and camera parameters to the another viewpoint
based on the depthmap. There are two steps involves in this process
1. Compute the optical flow / transformation of the pixels from the first
viewpoint to the second viewpoint based on the depthmap.
2. Splat the image pixels onto the transformed positions based on the
optical flow weighted by the depth.
Reference:
1. https://github.com/NagabhushanSN95/Pose-Warping
Args:
image: Input image tensor of shape (H, W, C)
depthmap: Depth map tensor of shape (H, W)
K1: Camera intrinsic matrix for the first camera of shape (3, 3)
K2: Camera intrinsic matrix for the second camera of shape (3, 3)
M1: Camera extrinsic matrix for the first camera of shape (4, 4)
M2: Camera extrinsic matrix for the second camera of shape (4, 4)
gamma: Scaling factor for the depth weights. Default is 3.0.
Returns:
Tuple[torch.Tensor, torch.Tensor]: A tuple containing:
- warped_image (torch.Tensor): The warped image tensor of
shape (H, W, C).
- mask (torch.Tensor): A mask tensor of shape (H, W)
indicating valid warped pixels.
"""
image = image.float()
height, width = image.shape[:2]
if K2 is None:
K2 = K1.clone()
# Step 1: Get optical flow
trans_coords = get_camera_transformation(depthmap=depthmap,
K1=K1,
K2=K2,
M1=M1,
M2=M2)
trans_depth = trans_coords[..., -1:] # z coordinates is the depth
uv_coords = get_uv_coords(height, width) # empty pixel coordinates
# Compute pixel flow
flow = (trans_coords[:, :, :2] / trans_depth) - uv_coords
# Step 2: Splat
# Get the depthmaps
depth_weights = get_weights_from_depthmap(depthmap=trans_depth,
gamma=gamma)
warped_image, mask = splat_points(image=image,
weights=depth_weights,
flowmap=flow)
# normalize the warped image
warped_image = warped_image.clamp(min=0, max=255)
warped_image = warped_image.round_().to(torch.uint8)
return (warped_image, mask, flow, depth_weights)
Lastly, the above implementation is differentiable with respect to the camera parameters and the depthmap, making is quite amenable to learning-based techniques as described in the beginning.
| [1] | Recall that camera pose estimation from a single image is an under-determined problem. There has been recent developments, like Mast3R, that address the problem of estimating the camera pose and the intrinsic parameters from 2 or more images based neural networks. The classical techniques often require either multiple () images (calibrated or in-the-wild) to estimate the camera parameters. |
| [2] | There has been some literature based on this idea - Check out Nvs-solver: Video diffusion model as zero-shot novel view synthesizer - ArXiv Link and Synsin: End-to-end view synthesis from a single image - ArXiv Link. |
| [3] | Another good article by Doan Huu Noi on this topic - Link. |
| [4] | Bao, W., Lai, W. S., Ma, C., Zhang, X., Gao, Z., & Yang, M. H. (2019). Depth-aware video frame interpolation. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. ArXiv Link |
| [5] | Niklaus, S., & Liu, F. (2020). Softmax splatting for video frame interpolation. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. ArXiv Link. |