RANSAC (RANdom SAmple Consensus) is a popular method for model estimation from a data with a large number of outliers. This belongs to a family of methods called robust estimation methods. Another example in this family is the least-median squares estimation. In this note, we shall discuss the RANSAC algorithm and a recently proposed improvement to it.

Problem Setting: Consider a dataset $\fD$ with $d-$dimensional points $\vx, \vy \in \R^d$ of size $N$. The data is known to have a significant number of outliers. The objective is to fit a model $f(\theta)$ accounting for the outliers in $\fD$.

For illustration, let us consider a simple 2D linear fitting. The figure shows a dataset with a lot of outliers with the ground truth and least-squares fit.

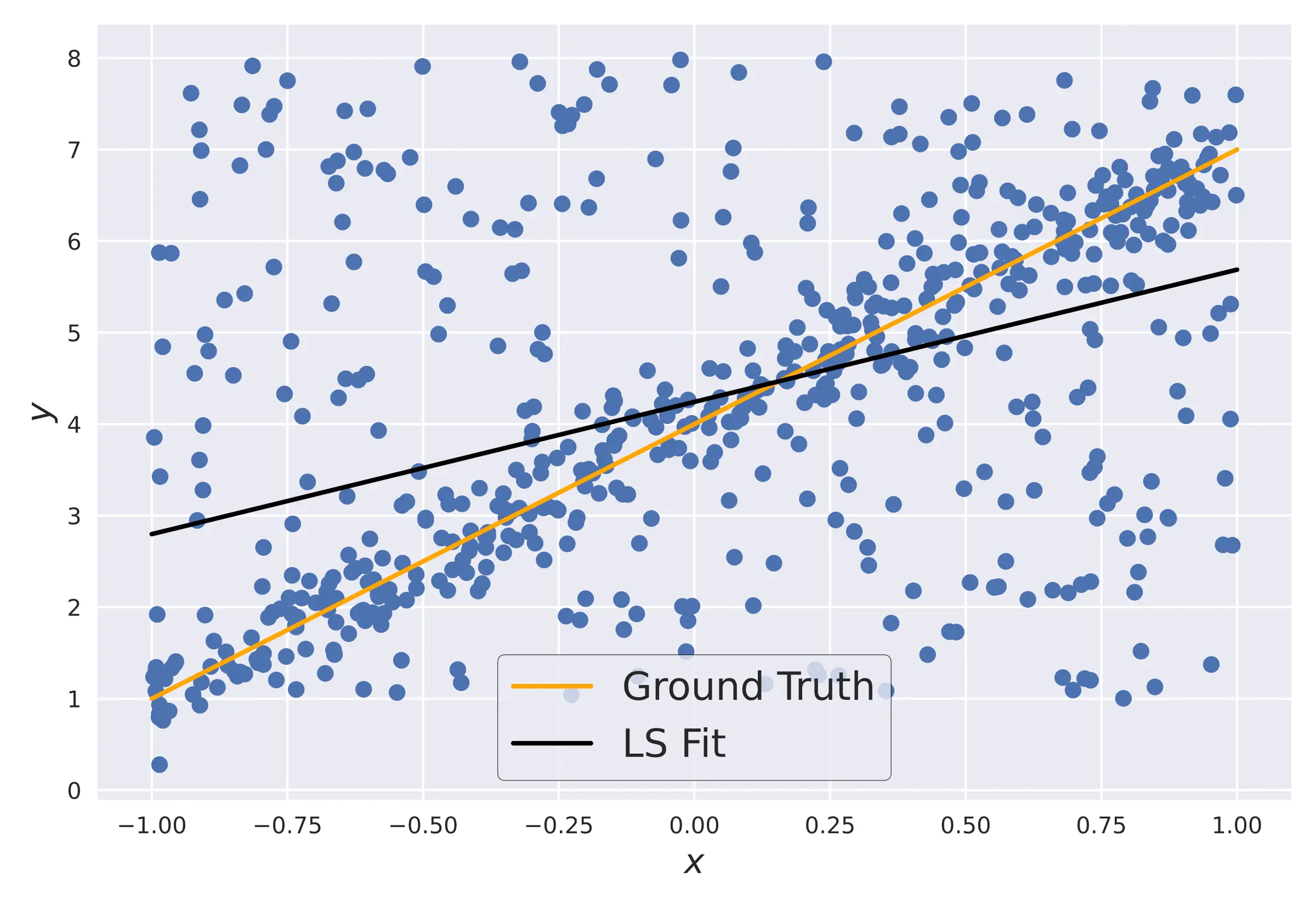
From the above figure, the usual least-squares estimate fails horribly. The more robust RANSAC algorithm proceeds as follows -

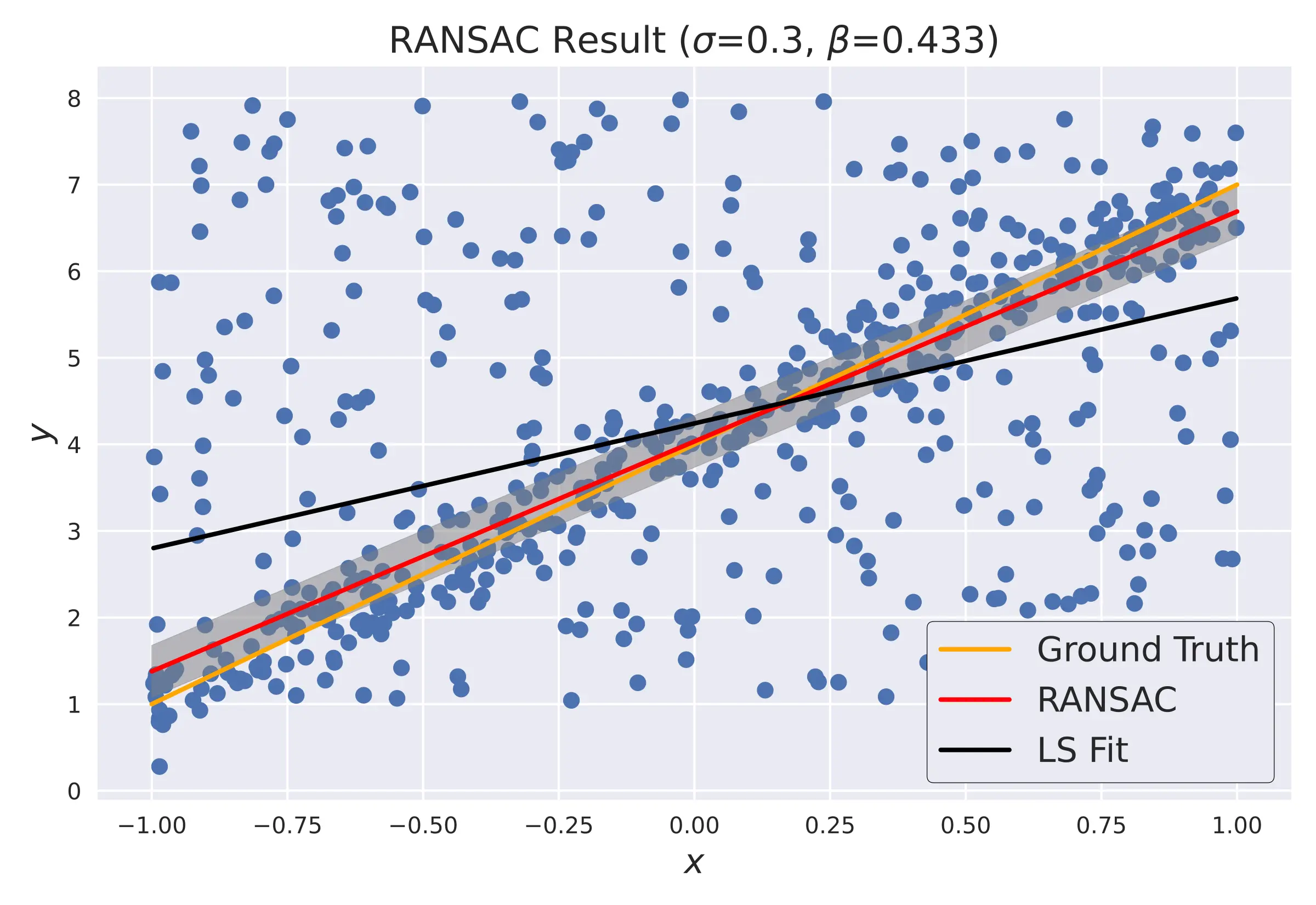
The above RANSAC algorithm has 3 main components (as highlighted above), the inlier-outlier threshold $\sigma$, the cutoff $\beta$ which specifies the probability of a point being an inlier in the given model, and the distance function $D$ which estimates the distance between the given point $(\vx_i, \vy_i)$ and the model $\theta$.

The number of iterations $T$ is given by $$ T = \frac{\log (1- \eta)}{\log \left (1 - \left(\frac{|\fI(\theta, \sigma, \fD)|}{|\fD|}\right)^S \right)} $$ Where the probability that a sampled point is an inlier is $|\fI(\theta, \sigma, \fD)|/|\fD|$ and $\eta$ is a user-defined confidence. $\eta$ is the probability that the RANSAC algorithm returns a good model after running.

Note that $1 - \left(\frac{|\fI(\theta, \sigma, \fD)|}{|\fD|}\right)^S$ is the probability that at least one of the points is an outlier in the subset $S$. So, $\left ( 1 - \left(\frac{|\fI(\theta, \sigma, \fD)|}{|\fD|}\right)^S\right)^T$ is the probability that the algorithm never selects $S$ inlier points, across $T$ iterations. This is the same as $1-\eta$. Taking log on both sides yields the above equation. One can quickly see that $T$ can be very large. But in practice, RANSAC is quite simple and fast and does not affect much in practice.

RANSAC Code

import jax # v0.4.26
import jax.numpy as jnp
from typing import Tuple

def dist(x1, y1, x2, y2, x, y):
    """
    Computes the distance of the point (x,y) from
    the line connecting the points (x1, y1) and
    (x2, y2).
    """
    num = (x2 - x1)*(y1 - y) - (x1 - x)*(y2 - y1)
    denom = jnp.sqrt((x2 - x1) **2 + (y2 - y1) ** 2)
    return jnp.fabs(num / denom)

def predict(w, x):
    """
    Simple Linear Model
    """
    return x@w

def fit(x, y):
    """
    Least Squares Fitting
    """
    return jnp.linalg.lstsq(x, y)[0]


def ransac(data: Tuple,
           S: int,
           sigma: float,
           beta:float) -> jax.Array:
    """
    RANSAC algorithm in JAX.

    Args:
        data (Tuple): x,y data points of length N
        S (int): Size of subset to sample (S < N)
        sigma (float): Inlier-outlier threshold
        beta (float): Fraction of inliers in the fitted model

    Returns:
        jnp.Array: Weights of the resultant model
    """

    x, y = data
    N = x.shape[0]
    assert S < N, "S must be less than N"
    # assert 0.0 < beta < 1.0 , "beta must be in (0.0, 1.0)"

    I = 0
    key = jax.random.key(42345)

    # def fwd():

    for _ in range(1000):
        # Sample a subset
        key, subkey = jax.random.split(key)
        i = jax.random.permutation(subkey,
                                   jnp.arange(x.shape[0]),
                                   independent=True)
        ids = i[:S]
        xs = x[ids]
        ys = y[ids]

        ws = fit(xs, ys)
        ys_pred = predict(ws, xs)
        dist_vec = lambda x__, y__: dist(xs[0],
                                   ys_pred[0],
                                   xs[-1],
                                   ys_pred[-1],
                                   x__,
                                   y__)
        d = jax.vmap(dist_vec)(x, y)[:, 0] # SIMD computation

        inds = jnp.where(d < sigma, True, False)
        I = inds.sum()

        if I > beta * N:
            d_final = d.copy()
            break

    # Fit the model on the final inlier set
    id_final = jnp.arange(d_final.shape[0])[d_final < sigma]

    x_final = jnp.ones((id_final.shape[0], x.shape[1]))
    y_final = jnp.zeros((id_final.shape[0], y.shape[1]))

    # print(x_final.shape, x.shape)
    x_final = x_final.at[:].set(x[id_final])
    y_final = y_final.at[:].set(y[id_final])

    w_final = fit(x_final, y_final)
    return w_final

MAGSAC : Marginalizing over the σ threshold

  One major difficulty of RANSAC in practice is choosing the value for the inlier-outlier threshold $\sigma$. This is a hard problem because, the threshold should ideally correspond to the noise level in the sought inliers and setting this threshold requires prior knowledge about the data and its geometry. The distance (albeit Euclidean), can still be unintuitive when the data lies on a higher dimensional manifold. Furthermore, the $\beta$ parameter, in a way, also depends on the $\sigma$. If the noise threshold is known and set correctly, then $\beta$ becomes irrelevant. The $\beta$ value can be viewed as accounting for the error in $\sigma$ value. But if the noise threshold is known, then we wouldn't really the RANSAC algorithm, would we? Naturally, There is a whole family of methods that address this noise level estimation.

The initial techniques, such as the RANSAAC, relied on model ensembles where a set of minimal sample models $\theta^\ast_1, \theta^\ast_2, \ldots, \theta^\ast_k$ are trained using the RANSAC algorithm each corresponding to $\sigma_1, \sigma_2, \ldots, \sigma_k$ and the final model $f(\theta^\ast)$ is obtained using weighted average of model parameters.

The next apparent extension is marginalization over the $\sigma$ parameter rather than relying on ensembles, as marginalization over $\sigma$ can be viewed as a generalization of ensembles. This avoids issues with the ensembles such as choosing appropriate weights for the ensembles. Secondly, the final model $f(\theta^\ast)$ can be obtained without a strict inlier/outlier decision. This is precisely what the MAGSAC (MArGinalizing SAmple Consensus) algorithm does^[1]. Interestingly, this makes it a Bayesian model^[2], although the authors didn't claim it to be one.

This paper, in my opinion, is a great example where a theoretical motivation is insufficient to lead to a proper algorithm. As such, the theoretical derivation of a $\sigma$-free model and the actual algorithm (the $\sigma-$consensus) are quite different. First, let's look at the marginalization part.

σ-Marginalization

  The distance metric can be thought of as computing the residuals of the model after fitting a subset of the input data. One issue with setting the $\sigma$ value manually is that the inlier is computed based on the distance metric, which depends on both the model, the distance metric, and the data distribution. The problem arises in our understanding of the role of $\sigma$. The inlier-outlier threshold is thought to be the same as the noise level in the data, according to the RANSAC algorithm. It is better to decouple them.

One way to resolve this is to set the inlier-outlier threshold based on the residuals computed by the distance metric. When the distance metric $D$ is euclidean, its square value follows a $\chi^2_m$ distribution (as $D^2$ is a sum of squared Gaussian variables), represented by the density $h(\vx, \vy)$, with degrees of freedom equal to the dimension of the data $d$. Based on this, we can say that a point is an inlier if it is in the 95% (0.95 quantile) of this $\chi^2$ distribution (from its inverse CDF). Specifically, the inlier-outlier threshold $\tau(\sigma) = H^{-1}_d(q) \sigma^{d}$ where $H$ is the CDF of the $\chi^2$ distribution and $q$ is set to a high quantile value like 0.95 or 0.99. Thus, based on the distance metric alone, we can obtain a way to set the noise threshold automatically.

Now that we have a way to set the threshold, let's look closely at the $\chi^2$ distribution $h(\vx, \vy)$ given by

$$ \begin{aligned} h(\vx, \vy | \sigma) &= 2C(d) \sigma^{-d}D^{d-1}(\theta, \vx, \vy) \exp \bigg (\frac{-D^2(\theta, \vx, \vy)}{2\sigma^2} \bigg ) \\ C(d) &= \frac{1}{2^{d/2}\Gamma(d/2)} \end{aligned} $$

Where $\Gamma$ is the Gamma function. This provides the likelihood of the point $\vx, \vy$ belonging to the model $\theta$, given the threshold $\tau(\sigma)$, based on the Euclidean distance metric $D$. If the point is an outlier, then the likelihood is 0.

$$ \begin{aligned} L(\vx, \vy | \theta, \sigma) = \begin{cases} h(\vx, \vy | \sigma) &, D(\vx, \vy, \theta) \geq \tau(\sigma)\\ 0 &, D(\vx, \vy, \theta) < \tau(\sigma) \end{cases} && \qquad \color{OrangeRed} (\text{Likelihood}) \end{aligned} $$

By marginalizing over $\sigma$, we can get the likelihood of the point simply being an inlier to the model.

$$ \begin{aligned} L(\vx, \vy | \theta) &= \int L(\vx, \vy | \theta, \sigma)\fU(0, \sigma_{\text{max}}) \; d\sigma = \int h(\vx, \vy | \theta, \sigma) \; \fU(0, \sigma_{\text{max}}) \; d\sigma \\ &= \frac{2C(d)}{ \sigma_{\text{max}}} \sum_{i=1}^K (\sigma_i - \sigma_{i-1}) \sigma_i^{-d} D^{d-1}(\vx, \vy, \theta) \exp \bigg (\frac{-D^2(\vx, \vy,\theta)}{2 \sigma_i^2} \bigg ) && \color{OrangeRed} (\text{Marginal Likelihood}) \end{aligned} $$

Where $\sigma_1 < \sigma_2 <\cdots < \sigma_K < \sigma_{\max}$. Interestingly, we can consider the likelihood as the importance or weight of that point and fit the model using the weighted least squares (WLS) algorithm.

σ-consensus algorithm

  Simply marginalizing away the $\sigma$ doesn't yield a proper algorithm. Note that even after marginalization, we still have to set a max noise level $\sigma_{\max}$ as an input parameter. This, however, is much easier to set than the noise threshold $\sigma$.

Given a max noise level in the data $\sigma_{\max}$, we can get the worse possible inlier set $\fI$ as the initial set, based on the given model $\theta$ and the inlier threshold is given by $\tau(\sigma_{\max})$. We then divide the max noise level into $m$ sub-levels $\sigma'$. When we encounter a data point that has a greater noise level than the current one, we update the model and the likelihood, and move onto the next noise level.

Model Quality

The procedure for getting the best model in the original RANSAC is based on the size of the consensus set. If the size of $\fI > \beta N$, then we terminate. More generally, we can construct a quality function $Q$ such that the higher the quality, the better the algorithm. We can define the quality function as the log likelihood of the model at a given noise level $\sigma$ $$ Q := \log L(\theta, \fD | \sigma) $$

For RANSAC, let $L_{\text{RANSAC}}(\theta, \sigma, (\vx, \vy))$ be the likelihood function of being an inlier (i.e. belonging to the consensus set), for a given noise level $\sigma$ at the given point $\vy, \vy$.

$$ \begin{aligned} L_{\text{RANSAC}}(\theta, \sigma, (\vx, \vy)) = \begin{cases} e &, D(\vx, \vy, \theta) \geq \sigma\\ 0 &, D(\vx, \vy, \theta) < \sigma \end{cases} && \quad \color{OrangeRed} (\text{RANSAC Likelihood}) \end{aligned} $$

We have chosen $e$ instead of $1$ for mathematical convenience as we will be taking the natural log later. It does not affect the result. The quality function can be obtained as

$$ \begin{aligned} Q_{\text{RANSAC}} &= \log \prod_{(\vx, \vy) \in \fD} L_{\text{RANSAC}}(\theta, \sigma, (\vx, \vy)) \\ &= \sum_{(\vx, \vy) \in \fD} \log L_{\text{RANSAC}}(\theta, \sigma, (\vx, \vy)) \\ &= \sum_{(\vx, \vy) \in \fI} \log L_{\text{RANSAC}}(\theta, \sigma, (\vx, \vy)) \\ &= |\fI(\theta, \sigma, \fD)| \end{aligned} $$

For MAGSAC, the likelihood of the model for each data point is given by equation (3). Marginalizing over $\sigma$, we get

$$ \begin{aligned} Q_{\text{MAGSAC}} &= \frac{1}{\sigma_{\max}}\int_0^{\sigma_{\max}} \log \prod_{(\vx, \vy) \in \fD}L(\vx, \vy | \theta, \sigma)\; d\sigma \\ &\approx \frac{1}{\sigma_{\max}} \sum_{i=1}^{K} \left [i (\log 2C(d)l - d\log \sigma_i) - \frac{R_i}{\sigma_i^2} + (d-1)B_i \right ](\sigma_i - \sigma_{i-1}) \end{aligned} $$

Where $R_i = 0.5 \sum_{j=1}^i D(\theta, (\vx_j, \vy_j))^2$ and $B_i = \sum_{j=1}^i \log D(\theta, (\vx_j, \vy_j))$.

Therefore, we terminate the MAGSAC iteration if a model of a desired quality has been obtained.

The MAGSAC algorithm improves upon the original RANSAC significantly enough to be added to the OpenCV library. The MAGSAC algorithm brings in the concept of the consensus set instead of an inlier set. However, the MAGSAC algorithm is slow, and requires a lot of iterations compared to the simple RANSAC. Interestingly, the authors suggest using the $\sigma-$ consensus algorithm once as a post-processing step for refining the RANSAC result to get an even better model.