Converting Between Perspective and Equirectangular Projections

Inverting the common procedure of converting equirectangular images to perspective images.

Recently I had a task to convert between perspective and equirectangular projections. Equirectangular projections can be found in VR and 360 degree image/video content. Although there are more efficient projection available today for 360 media content^[1], equirectangular remains the simplest and a widely supported format. In any case, it is a good first projection to understand before moving onto the more sophisticated ones.

Perspective Projection

Perpsective projections are what you get when you take a photo of your camera. Objects that are further away from the camera appear smaller and all the lines appear to project toward vanishing points (i.e. where the parallel lines seem to converge).

Recall that the Pinhole Camera model (bet used for a perspective projection), where some real-world point $p$ with coordinates $(x, y,z)$ is projected onto the image plane at $(u, v)$ as

$$ \begin{aligned} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \begin{bmatrix} f_x & 0 & 0 & c_x \\ 0 & f_y & 0 & c_y \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\\ &= KR \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \end{aligned} $$

Where $K$ is the intrinsic camera matrix, $R$ is the extrinsic camera matrix, $f_x, f_y$ are the focal lengths of the camera, $c_x, c_y$ define the optical centre, and $t_1, t_2, t_3$ are the translation components ^[2]. Therefore, given the matrices $K$ and $R$, we can convert between pixel coordinates and the world coordinates. A quick not about the axis convention - the $z-$axis is the optical axis of the camera, the $x-$axis is the horizontal axis, and the $y-$axis is the vertical axis.

def camera_to_world(points: np.ndarray, K: np.ndarray, R:np.ndarray) -> np.ndarray:
    """

    Transforms the given 3D points from camera coordinates to world coordinates

    Args:
        points (np.ndarray): 3D points in homogeneous camera coordinates
        K (np.ndarray): 3x3 matrix representing the intrinsic camera matrix
        R (np.ndarray): 3x3 matrix representing the extrinsic camera matrix (rotation)

    Returns:
        world_points (np.ndarray): 3D points in world coordinates

    """

    K_inv = np.linalg.inv(K)

    world_points = (points @ K_inv.T) @ R.T
    return world_points


def world_to_camera(points: np.ndarray, K: np.ndarray, R:np.ndarray) -> np.ndarray:
    """

    Transforms the given 3D points from world coordinates to camera coordinates

    Args:
        points (np.ndarray): 3D points in world coordinates
        K (np.ndarray): 3x3 matrix representing the intrinsic camera matrix
        R (np.ndarray): 3x3 matrix representing the extrinsic camera matrix (rotation + translation)

    Returns:
        camera_points (np.ndarray): 3D points in camera coordinates
    """

    # Add translation to the rotation matrix
    # As of now, the translation is zero.
    R = np.hstack([R, np.array([[0,0,0]], np.float32).T])

    camera_points = (points @ R.T) @ K.T
    return camera_points

To get the camera matrix $K$ from a given image, we only need two parameters - the field-of-view (FOV) and the image dimensions $(W, H)$. The focal lengths $f_x$ and $f_y$ can be computed from the FOV as

$$ f_x =f_y = \frac{W}{2 \tan (\text{FOV}/2)} $$

def get_camera_matrix(FOV: float, width: int, height: int) -> np.ndarray:
    """

    Computes the intrinsic camera matrix from the given camera
    field of view (FOV) and image/window dimensions.

    Args:
        FOV (float): Field of view in radians
        width (int): Image/window width
        height (int): Image/window height

    Returns:
        K (np.ndarray): 3x3 matrix representing the intrinsic camera matrix
    """

    f = 0.5 * width / np.tan(0.5 * FOV)
    cx = (width) / 2.0
    cy = (height) / 2.0

    K = np.array([
            [f, 0, cx],
            [0, f, cy],
            [0, 0, 1]]).astype(np.float32)

    return K

def get_extrinsic_matrix(THETA:float, PHI:float):

    # Default
    elevation_vector = np.array([0.0, THETA, 0.0], np.float32)
    azimuth_vector = np.array([PHI, 0.0, 0.0], np.float32)

    # Use Rodrigues' formula to convert the
    # angle vector (simulatenous) to rotation matrix
    R1, _ = cv2.Rodrigues(elevation_vector)
    R2, _ = cv2.Rodrigues(np.dot(R1, azimuth_vector))

    R = R2 @ R1
    return R

Equirectangular Projection

Equirectangular projections are derived from the Spherical camera model and not the Perspective (linear) model discussed above.

Mapping from 3D world coordinates $p$ to 2D equirectangular coordinates $(x_{eq}, y_{eq})$ is a two-step procedure. Since the Equirectangular projection is a projection of a sphere unto a 2D surface, we first convert the 3D world coordinates to spherical coordinates $(\theta, \phi)$ as

$$ (\theta, \phi) = \left ( \text{atan2} (x, z), \arcsin \left (\frac{y}{\rho} \right ) \right ) $$

Where $\rho = \sqrt{x^2 + y^2 + z^2}$, $\theta$ is the Azimuth angle, and $\phi$ is the elevation angle. The Azimuth is also called as the longitude and the elevation the latitude in map projections.

def cartesian_to_spherical(points: np.ndarray) -> np.ndarray:
    """
    Converts the given 3D points from cartesian coordinates to spherical coordinates

    Args:
        points (np.ndarray): 3D points in cartesian coordinates

    Returns:
        sp_coords (np.ndarray): 3D points in spherical coordinates (rho, theta, phi)
    """

    assert points.shape[-1] == 3, "Input should have 3 (X, Y, Z) components"

    x, y, z = points[..., 0], points[..., 1], points[..., 2]

    # Distance of points from the origin
    rho = np.linalg.norm(points, axis=-1)

    # Normalize the points on the sphere of the above radius
    # to get the points on the unit sphere
    x /= rho
    y /= rho
    z /= rho

    # Elevation angle (aka latitude)
    phi = np.arcsin(y)

    # Azimuthal angle (aka longitude)
    theta = np.arctan2(x, z)

    # return np.stack([rho, theta, phi], axis=-1)
    return np.stack([rho, theta, phi]).T


def spherical_to_cartesian(sp_coords: np.ndarray) -> np.ndarray:
    """
    Converts the given 3D points from spherical coordinates to cartesian coordinates

    Args:
        sp_coords (np.ndarray): 3D points in spherical coordinates (rho, theta, phi)

    Returns:
        points (np.ndarray): 3D points in cartesian coordinates
    """

    assert sp_coords.shape[-1] == 3, "Input should have 3 (rho, phi, theta) components"

    rho = sp_coords[..., 0]
    theta = sp_coords[..., 1]
    phi = sp_coords[..., 2]

    x = rho * np.cos(phi) * np.sin(theta)
    y = rho * np.sin(phi)
    z = rho * np.cos(phi) * np.cos(theta)

    return np.stack([x, y, z], axis=-1)

Next, the above spherical cooridinates are mapped to the 2D equirectangular coordinates $(x_{eq}, y_{eq})$ as

$$ \begin{aligned} x_{eq} &= \left ( \frac{\theta + \pi }{ 2\pi} \right ) W \\ y_{eq} &= \frac{H}{\pi} \left ( \phi + \frac{\pi}{2} \right ) \end{aligned} $$ Where $W$ and $H$ are the width and height of the equirectangular image respectively. Let's take a minute to quickly demystify the above formula. The $\phi=0$ latitude and $\theta=0$ longitude corresponds to the center of the equirectangular image $ \Rightarrow x_{eq} = W /2, y_{eq} = H/2$. Furthermore, according to practical convention, "upwards" is positive and "downwards" in negative. Therefore, the $\phi$ and $\theta$ are normalized to the ranges $[-\pi, \pi]$ and $[-\pi/2, \pi/2]$ respectively, and mapped to the 2D image with a offset equal to half of their corresponding range.

As the ranges of $\theta$ and $\phi$ have the ratio 2:1, the resultant equiangular image will have a 2:1 aspect ratio as well, hence the name Equi-rectangular.

def spherical2equirect(sp_coords: np.ndarray,
                       width: int,
                       height: int)-> np.ndarray:
    """
    Args:
        sp_coords (np.ndarray): Spherical coordinates (theta, phi, rho)
        width (int): Width of the equirectangular image
        height (int): Height of the equirectangular image

    Returns:
        np.ndarray: Equirectangular coordinates (x, y)
    """

    rho, theta, phi = sp_coords[..., 0], sp_coords[..., 1], sp_coords[..., 2]
    x = (theta / (2 * np.pi) + 0.5) * (width)
    y = (phi / (np.pi) + 0.5) * (height)

    return np.stack([x, y], dtype=np.float32).transpose(2, 1, 0) # (width, height, 2)

As evident from the above formula, the resultant mapping to the 2D plane is a distorted one, with the poles of the sphere being stretched out. However, compared to other similar cylindrical projections like the Mercator or the Lambert's, the equirectangular is the simplest as the latitude and longitudes are directly mapped to the 2D plane. As a result, the latitude and longitude lines appear as a regular (equidistant) grid. This is in contrast to the actual longitudinal lines that get closer to each other as they approach the poles. Nontheless, this projection is widely used in panoramic photography to create immersive 360-degree images.

Equirectangular to Perspective

With the above knowledge, we can easily convert a given equirectangular image to a perspective image. Converting from equirectangular to perspective is useful when a natural looking portion of the image is required. For example, in a VR application, the user's head movement can be used to render the perspective image from the equirectangular image.

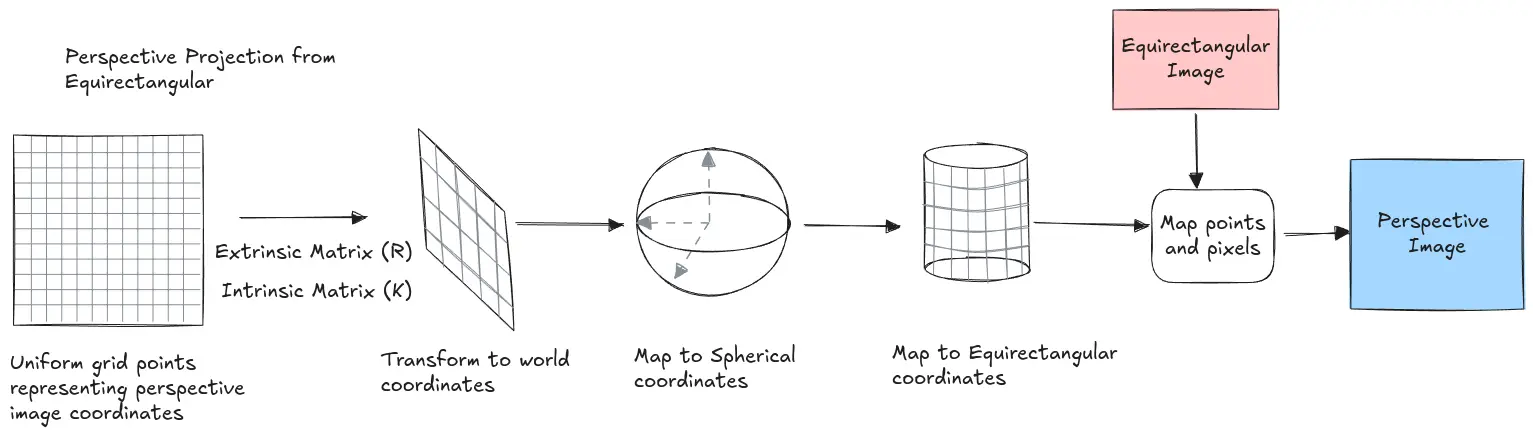
Equirectangular to Perspectivce Projection

Procedure for mapping from Equirectangular to Perspective projection.

The procedure is as follows -

Generate a uniform grid of points that represent the perspective image.
Convert the grid points to world coordinates using the camera matrix $K$ and the extrinsic matrix $R$.
Convert the world coordinates to spherical coordinates using the cartesian_to_spherical function.
Convert the spherical coordinates to equirectangular coordinates using the spherical2equirect function.
Use the cv2.remap function to generate the perspective image with the above equirectangular coordinates.

def Equirec2Perspec(img:np.ndarray,
                    FOV: float,
                    THETA: float,
                    PHI: float,
                    height: int,
                    width:int) -> np.ndarray:
    """
    Args:
        img (np.ndarray): Equirectangular image
        FOV (float): Field of view in degrees
        THETA (float): Elevation angle in degrees
        PHI (float): Azimuthal angle in degrees
        height (int): Height of the perspective image
        width (int): Width of the perspective

    Returns:
        Perspective image
    """

    # Convert the angles to radians
    FOV = np.deg2rad(FOV)
    THETA = np.deg2rad(THETA)
    PHI = np.deg2rad(PHI)

    img_height, img_width = img.shape[:2]
    # Compute the intrinsic camera matrix
    K = get_camera_matrix(FOV, width, height)

    # Compute the extrinsic matrix
    R = get_extrinsic_matrix(THETA, PHI)

    # Generate the image grid
    x, y = np.meshgrid(np.arange(width), np.arange(height))

    # Convert the image grid to homogeneous coordinates
    z = np.ones_like(x)
    xyz = np.concatenate([x[..., None], y[..., None], z[..., None]], axis=-1)

    # Convert the image grid to world coordinates
    world_coords = camera_to_world(xyz, K, R)

    # Convert the world coordinates to spherical coordinates
    sp_coords = cartesian_to_spherical(world_coords)

    # Convert the spherical coordinates to image coordinates
    XY = spherical2equirect(sp_coords, img_width, img_height)

    # Generate the perspective image
    persp = cv2.remap(img, XY[..., 0], XY[..., 1], cv2.INTER_CUBIC, borderMode=cv2.BORDER_WRAP)


    return persp

Perspective to Equirectangular

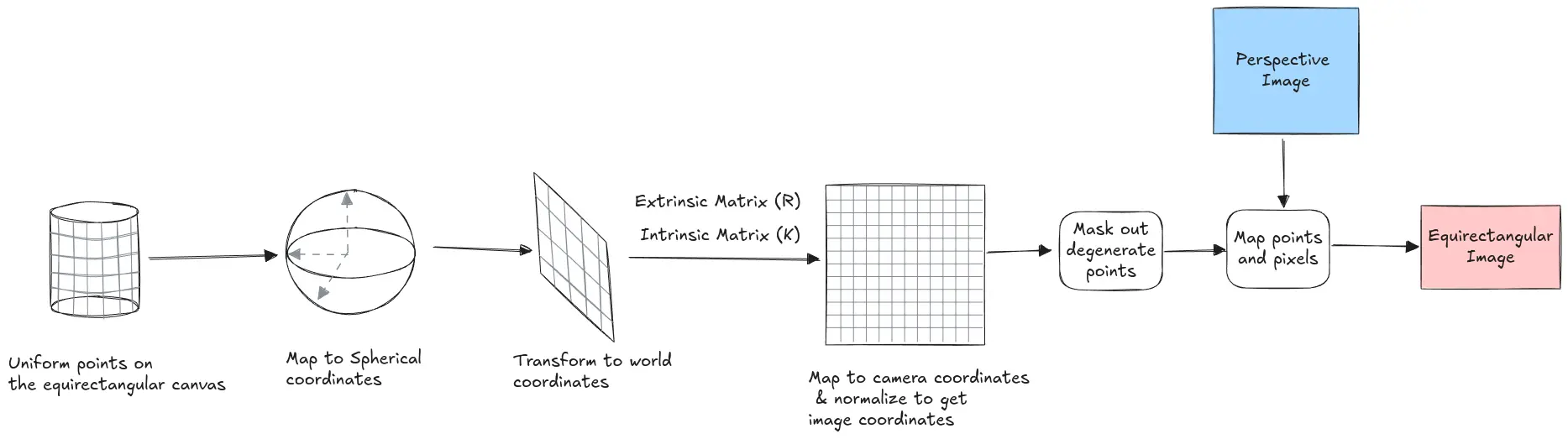
Procedure for mapping from Perspective to Equirectangular projection.

The procedure for mapping from perspective to equirectangular (illustrated above) is as follows

Generate a uniform grid of points that represent the equirectangular image. This can be done by generating a grid of points between $[0, 1]$ and mapping them top the spherical coordinates.
Convert the uniform spherical coordinates to Cartesian (world) coordinates using the spherical_to_cartesian function.
Convert the world coordinates to camera coordinates using the world_to_camera function and the camera matrix $K$ and the extrinsic matrix $R$.
Project the camera coordinates to the image plane and normalize the x, y coordinates.
Mask out the degenerate points that are "behind" the camera and outside the image plane. Note that since we sampled uniformly from the sphere, there is no guarantee that all those points will be visible in the perspective image.
Use the cv2.remap function to generate the equirectangular image with the above camera coordinates.


def Perspec2Equirec(img: np.ndarray,
                    FOV: float,
                    THETA:float,
                    PHI:float,
                    height:int,
                    width:int) -> np.ndarray:
  """

  Args:
          img (np.ndarray): Perspective image
          FOV (float): Field of view in degrees
          THETA (float): Elevation angle in degrees
          PHI (float): Azimuthal angle in degrees
          height (int): Height of the output equirectangular image
          width (int): Width of the output equirectangular image

  Returns:
          Equirectangular image (np.ndarray)
  """

  # Convert the angles to radians
  FOV = np.deg2rad(FOV)
  THETA = np.deg2rad(THETA)
  PHI = np.deg2rad(PHI)

  img_height, img_width = img.shape[:2]

  K = get_camera_matrix(FOV, img_width, img_height)
  R = get_extrinsic_matrix(THETA, PHI)

  # Invert the extrinsic matrix (its orthogonal)
  R = R.T

  # Generate the grid points for the equirectangular image
  u, v = np.meshgrid(np.linspace(0,1,width), np.linspace(0,1,height))

  # Map the above equirect coordinates to spherical coordinates
  theta = 2 * np.pi * (u - 0.5)
  phi = np.pi * (v - 0.5)

  # The above block is equivalent to
  # theta, phi = np.meshgrid(np.linspace(-np.pi, np.pi, width), np.linspace(-np.pi/2, np.pi/2, height))

  # Construct the spherical Coordinates
  sp_coords = np.stack([np.ones_like(theta), theta, phi], axis=-1)

  # Convert the spherical coordinates to cartesian (world) coordinates
  coords = spherical_to_cartesian(sp_coords).astype(np.float32)

  # Make the world coords homogeneous
  coords = np.append(coords, np.ones_like(coords[..., :1]), axis=-1)

  # Map the world coordinates to camera coordinates
  camera_coords = world_to_camera(coords, K, R)

  # Project and x, y coordinates to the image plane and normalize
  uv = camera_coords[..., :2] / camera_coords[..., 2:3]
  uv = uv.astype(np.float32)

  # Mask out the points that are "behind" the camera
  mask = camera_coords[..., 2] > 0

  mask *= np.where((uv[..., 0] >= 0)&
          (uv[...,0] < img_width)&
          (uv[...,1] >= 0)&
          (uv[...,1] < img_height), True, False)

  equirec = cv2.remap(img, uv[..., 0], uv[...,1], cv2.INTER_CUBIC, borderMode=cv2.BORDER_WRAP)

  equirec *= mask[..., None]
  return equirec

Equirectangular to Perspective Projection

Mapping from Perspective to Equirectangular and back

[1]

Cubemaps are another popular 360 degree projection format. Google's Equiangular Cubemap (EAC) have become quite popular for efficient and others like GoPro have even adopted this format. For map projections, although Equirectagnular is one of the oldest, due to its high distortion (neither areas nor angles between cruves are preserved), it is seldom used.

[2]	A couple of good references for camera model and their history can be found here and here.